2-6:串列、陣列與張量
我們前面的單元,有提到串列(list)搭配迴圈的計算,所使用到的是一維串列。串列也可以是二維、三維或更高維,在統計分析和繪製圖表經常會接觸到,它的功能就類似別種語言的陣列。
但它在某些方面卻有迥然不同的運算方式,即以最簡單的加法而言,它的結果也出乎一般初學者的預料。比如我們把兩個一維串列(向量)相加,[1,2,3]+[4,5,6],竟然會得到[1,2,3,4,5,6]。
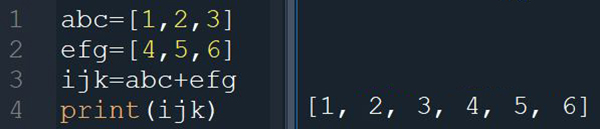
這樣的運算是有它的用意的。第一,它可以把分次得到的資料整理在一起;第二,它可以擁有記憶的功能。
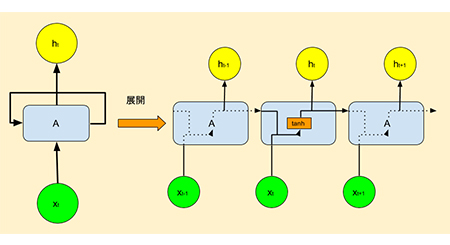
下圖是我們先前提到的循環神經網路RNN,在右邊展開的三個時序圖中,我們可以看到,前面時序處理過的訊息,會和最新輸入的訊息結合在一起後,再做下一步的處理。這兩個訊息結合在一起,使用的就是類似這種串列加法的連接運算(concatenate),這種運算可以把新舊記憶連結起來。
如果堅持一定要使用線性代數的計算方式,就要使用到Python裡面運算功能強大的套件模組–Numpy,Numerical python。它的核心是使用C語言來開發的,很適合快速處理大量資料。
下圖第5行先匯入numpy模組並簡化其命名為np,第6、7行利用np的array函式,將串列轉換成陣列,經過加總後再輸出,就可以得到一般線性代數計算的結果。
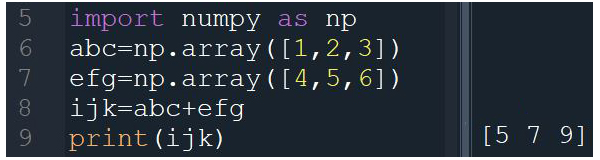
但numpy的功能遠不止於這些,它在數學觀念上的轉變,和程式碼裡面符號的處理,是有相當程度的躍升了。
早在Matlab最活耀的時代,它已經把矩陣的符號轉換成適合程式碼輸入的形式。例如一個最簡單的3×3影像矩陣,將其灰階值表示成[25 33 120;18 95 212;130 77 255],這種矩陣表示方式可稱之為二維陣列。很顯然的,這樣的數據要輸入程式碼中是沒有問題的。相較之下,傳統的矩陣符號,是不太適合寫成程式碼的,
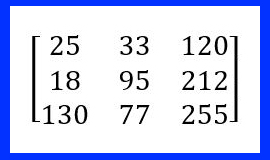
圖2-6-4. 傳統的矩陣表示方式,把數據夾在兩個大型中括弧內,並不適合寫成程式碼。
到了numpy的階段,它把上式二維陣列,再進一步轉換,寫成更精準的模樣,這就是所謂的ndarray(n-dimensional array),[[25 33 120] [18 95 212] [130 77 255]]。
這種寫法,極具擴充性,我們可以把它擴充成四維陣列,[[[[25] [33] [120]] [[18] [95] [212]] [[130] [77] [255]]]]。增加的外層維度(藍色)意思是說,除了這張影像,還可以再置入其他影像;增加的內層維度(橘色)意思是說,裡面的灰階值,可以從單一灰階值,擴充成紅綠藍三種灰階值。
嚴格來講,這邊的維度應該叫做軸度(axis)。在numpy裡面,維度(dimension),指的是向量裡面元素的個數。經常聽到的名詞「降維」(dimensionality reduction),其實是減少元素個數,來提取特徵。
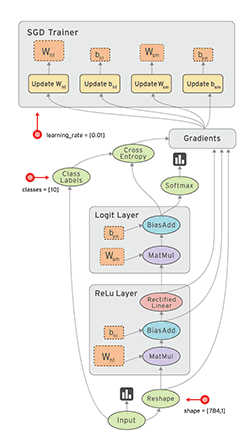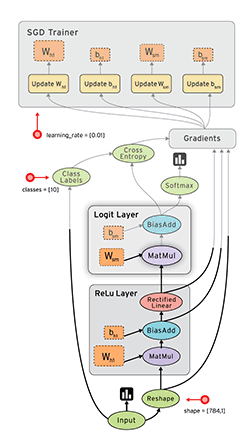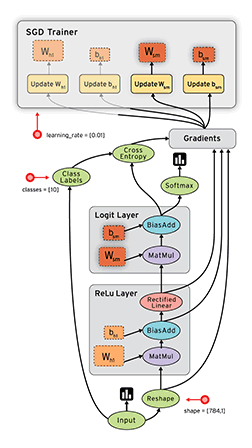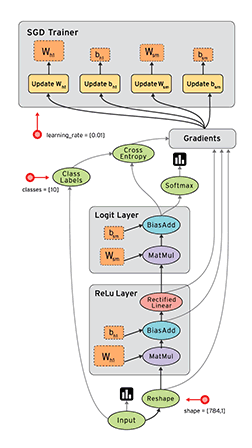
最後,必須提到上圖TensorBoard中張量(tensor)的概念。tensor在很多方面都類似ndarray,但它是專為深度學習而設計,可運行在GPU上面,而ndarray比較常使用到CPU。
Google的深度學習框架(framework),叫做TensorFlow,數據在上一神經層運算完畢後,再進入到下一神經層處理,好像張量在流動一樣。
在實務工作上,TensorFlow常是深度學習工程師必備工具,但它跨入門檻不低,所以在學術研究上,很多人喜歡用臉書公司開發的技術Pytorch來發表論文。
