3-2:監督式學習之瓶頸
監督式學習,好像是學生在準備社會科考試一樣,唸的題目越多,背的標準答案越多,答題的準度和分數就會越高。但是要從90分考到95分,究竟要再多記憶多少內容,沒有人能提出精準的數據評估,甚至多背些考題是否一定就會提高分數,也很難講。
而且,除了記憶事物之外,舉一反三、觸類旁通的能力也很重要啊!它讓我們可以從有限的記憶中,摸索推理出不曾背誦過的資訊,這也許是人類智慧中更重要的部份。
例如有個題目問,“美國第一大都市在哪裡?”,我們很快可以回答是“紐約市”。如果再問“紐約在荷蘭人佔領期間的名稱是甚麼?”,或者“新阿姆斯特丹的北城牆,為現今金融中心的甚麼街?”,這些加以思考推理或許就可得到的答案,監督式學習必須輸入更多的資料來訓練,否則無法回答。
所以有好事者比喻,一味地只知道使用監督式學習,就像是古代巴比倫人建好巴別塔,自認為已經可以通達天際了,實際上還差了十萬八千里。

圖3-2-1. 古巴比倫人建立的巴別塔,高聳入雲霄,他們認為可以藉此和天際溝通了。
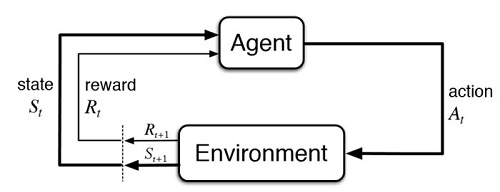
這個時候,強化式學習就可以提供有價值的處理方向了。
強化式學習,訓練次數少則數十回合(episode),多則數萬甚至數百萬回合。剛開始訓練的少數回合當中,在做決定過程時,會有比較多的隨機選擇,等到訓練過較多的回合了,能夠藉以參考的數據足夠了,就會逐漸增加自我判斷的比率,同時持續減少隨機選擇的次數。
這隨機選擇的功能,就程式設計而言,是要避免它無法跳脫不定次數迴圈;就策略規劃而言,是希望它儘量嘗試各種可能性,以真正找出最佳的報酬策略,這當中自然就會帶有一些推理成份了。
下面的9×9迷宮遊戲,主角起始位置在迷宮正中央,右下角格子的reward=+30,代表寶藏地點,找到這裡該回合即結束;左上角格子的reward= – 30,是大魔王地點,抵達此處會被吃掉,該回合同樣結束。黑色格子是不可穿越之障礙區,其餘格子皆reward= – 0.2,所以每多走一步都會被扣0.2,要用最少的步數才能得到最大的報酬(return)。
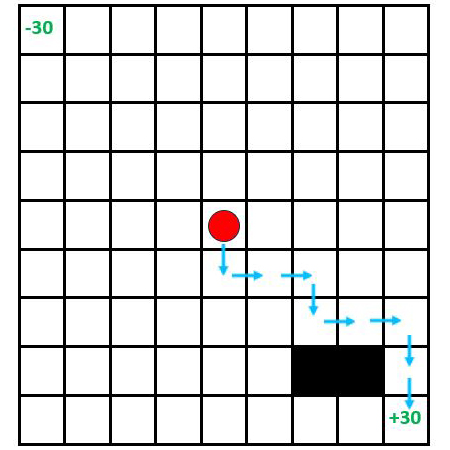
圖3-2-2. 一個9×9的迷宮遊戲,希望用最少的步數,讓主角由正中央的起始位置,找到右下角寶藏地點。
我們第一次執行模型,讓它跑100個回合,並刻意使其隨機選擇的比率以較快的速度減少,發現它要找到最佳步數的8次會比較吃力。

第二次同樣讓模型跑100個回合,但讓它的隨機選擇以較慢的速度減少,發現它的訓練成效有改善了。